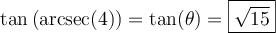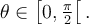3.3 Fonctions trigonométriques inverses
- Introduction
- Fonction arcsin
- Fonction arccos
- Fonction arctan
- Autres fonctions trigonométriques inverses
- Résoudre une équation trigonométrique
5. Fonctions arcsec, arccot et arccsc
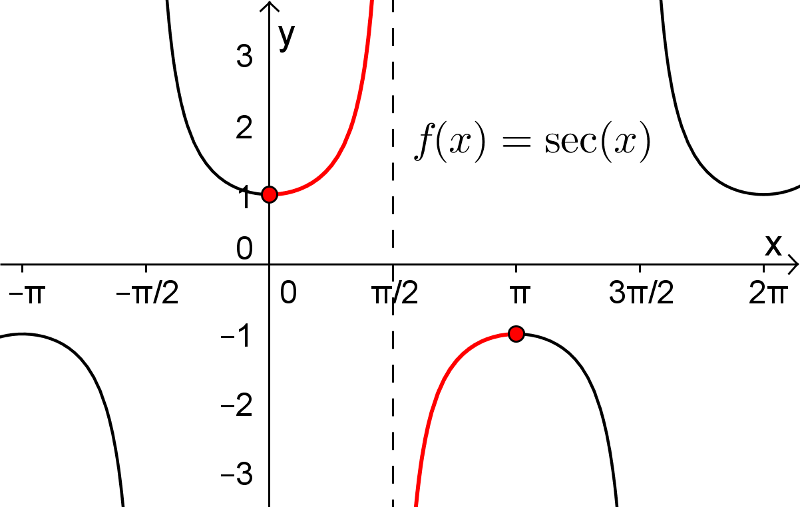
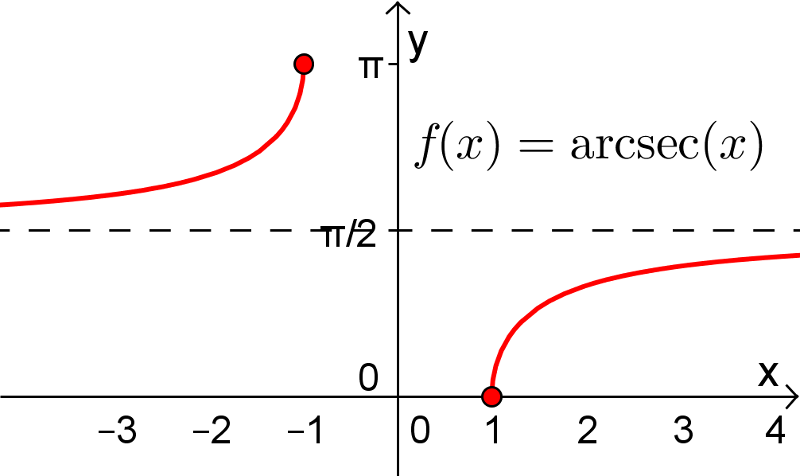
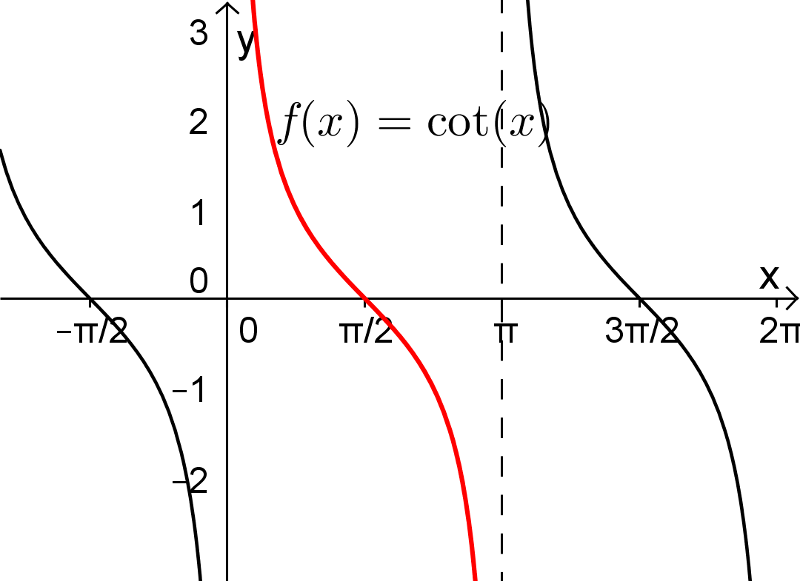
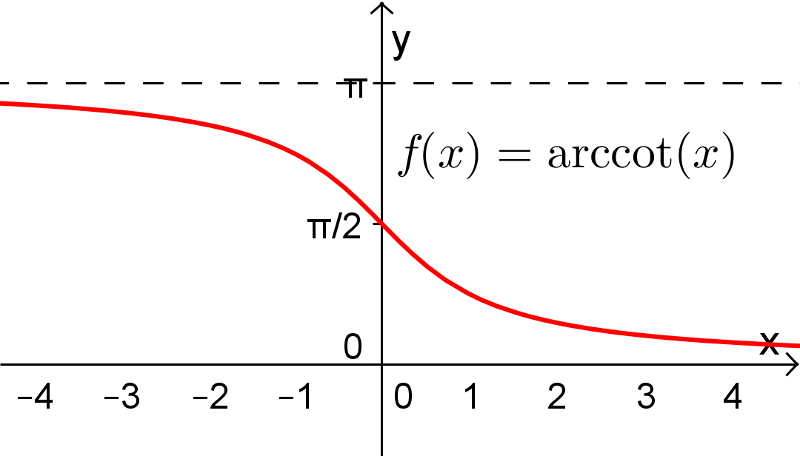
Les fonctions sécante, cotangente et cosécante possèdent également leurs fonctions réciproques sur un intervalle restreint de leur domaine. Pour les fonctions arcsec et arccsc, le choix de l'intervalle restreint pour  ne fait pas l'unanimité chez plusieurs mathématiciens en raison du signe de la dérivée de ces fonctions. Tout cela vous sera expliqué dans votre cours Calcul différentiel. Voici les définitions de ces trois dernières fonctions réciproques.
ne fait pas l'unanimité chez plusieurs mathématiciens en raison du signe de la dérivée de ces fonctions. Tout cela vous sera expliqué dans votre cours Calcul différentiel. Voici les définitions de ces trois dernières fonctions réciproques.
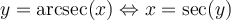
![y\in\left[0,\frac{\pi}{2}\right[\cup\left]\frac{\pi}{2},\pi\right] y\in\left[0,\frac{\pi}{2}\right[\cup\left]\frac{\pi}{2},\pi\right]](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/c7b1a86e07a554cbcd2afa6c5641e6ad.png)
![\text{dom}(\text{arcsec})=]-\infty,-1]\cup[1,\infty[ \text{dom}(\text{arcsec})=]-\infty,-1]\cup[1,\infty[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/3c78b49eb2f0926e4a7d3f5ff72c79d7.png)
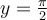

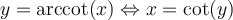
![y\in\left]0,\pi\right[ y\in\left]0,\pi\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/81a8984d324c8954afbb0dd54d7216cd.png)
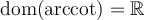
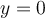
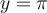
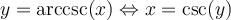
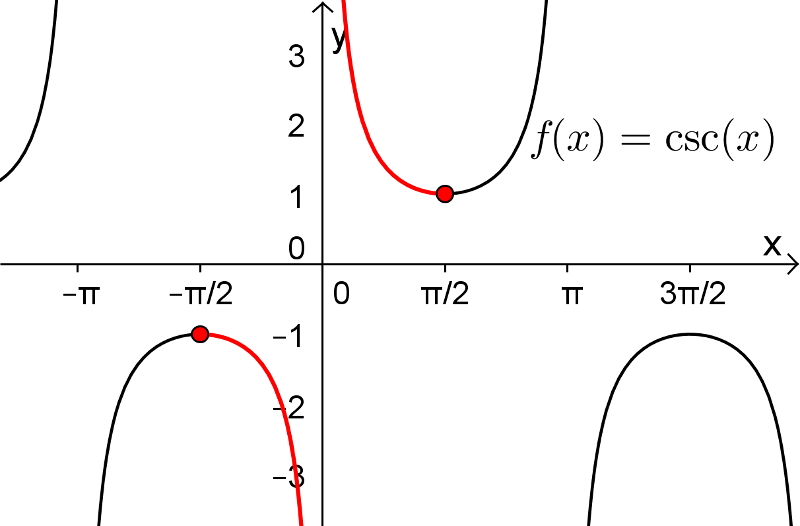
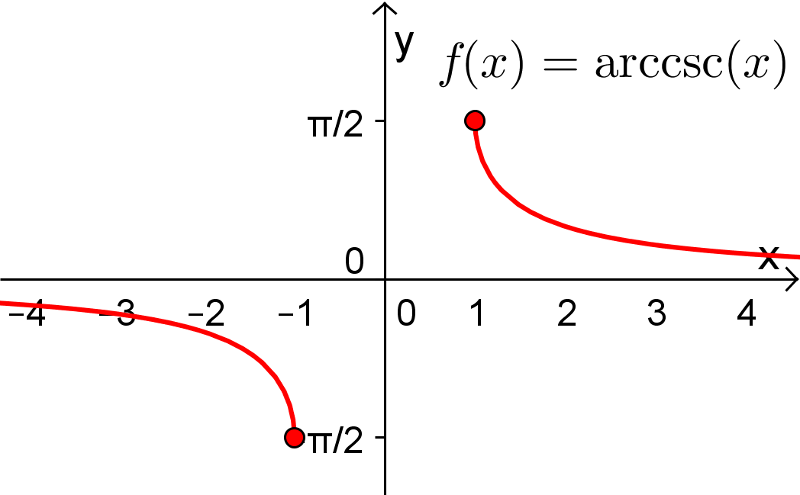
![y\in\left[-\frac{\pi}{2},0\right[\cup\left]0,\frac{\pi}{2}\right] y\in\left[-\frac{\pi}{2},0\right[\cup\left]0,\frac{\pi}{2}\right]](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/cb21661f30a4dae2fe502249dacd3715.png)
![\text{dom}(\text{arccsc})=\left]-\infty,-1]\cup [1,\infty\right[ \text{dom}(\text{arccsc})=\left]-\infty,-1]\cup [1,\infty\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/c472018bddbce3a41f4f1804bec64b01.png)
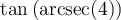
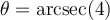
![\theta\in\left[0,\pi\right]\setminus\left\lbrace\frac{\pi}{2}\right\rbrace \theta\in\left[0,\pi\right]\setminus\left\lbrace\frac{\pi}{2}\right\rbrace](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/8625cfdf1b563518029ab545d1a0d25c.png)
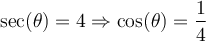
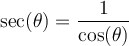
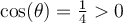
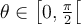

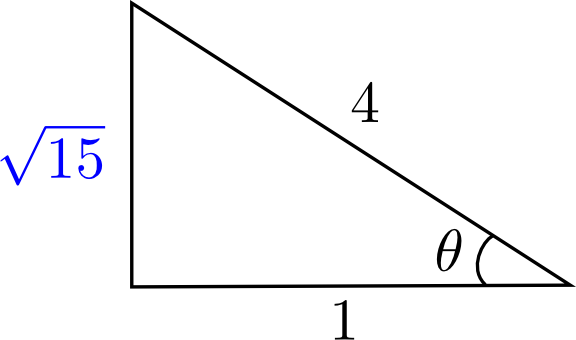
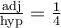
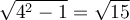
![\begin{array}{rll}\tan\left(\text{arcsec}(4)\right)&=\tan(\theta)&\small\text{; car }\theta=\text{arcsec}(4)\\&=\dfrac{\sqrt{15}}{1}&\small\text{; car }\tan(\theta)=\frac{\text{opp}}{\text{adj}}\\[1em]&=\sqrt{15}&\end{array} \begin{array}{rll}\tan\left(\text{arcsec}(4)\right)&=\tan(\theta)&\small\text{; car }\theta=\text{arcsec}(4)\\&=\dfrac{\sqrt{15}}{1}&\small\text{; car }\tan(\theta)=\frac{\text{opp}}{\text{adj}}\\[1em]&=\sqrt{15}&\end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/f80624bf3e856c7eb7ede980a00d7ba4.png)