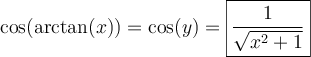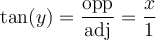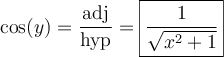3.3 Fonctions trigonométriques inverses
- Introduction
- Fonction arcsin
- Fonction arccos
- Fonction arctan
- Autres fonctions trigonométriques inverses
- Résoudre une équation trigonométrique
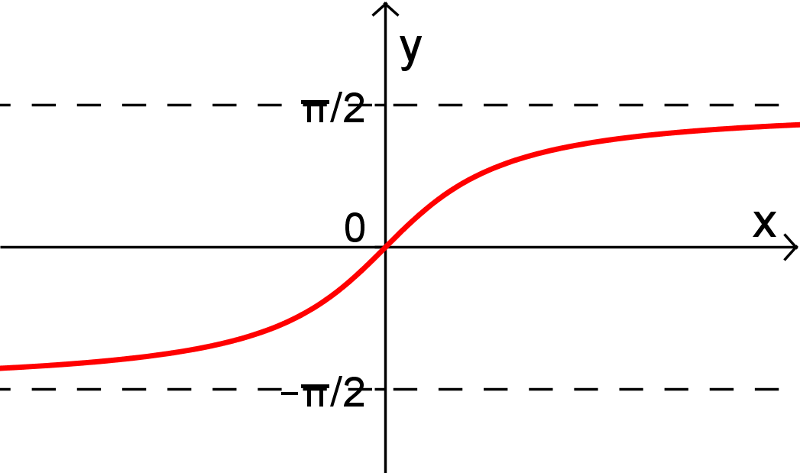
4. Fonction arctan
On peut rendre la fonction tangente injective en restreignant son domaine aux valeurs ![x\in\left]-\frac{\pi}{2},\frac{\pi}{2}\right[ x\in\left]-\frac{\pi}{2},\frac{\pi}{2}\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/6eb648a9b0954c2e5b4b51ea4a961853.png) , comme on peut le voir dans les figures suivantes. La fonction arctangente est donc la réciproque de cette fonction injective et est représentée par la courbe rouge.
, comme on peut le voir dans les figures suivantes. La fonction arctangente est donc la réciproque de cette fonction injective et est représentée par la courbe rouge.
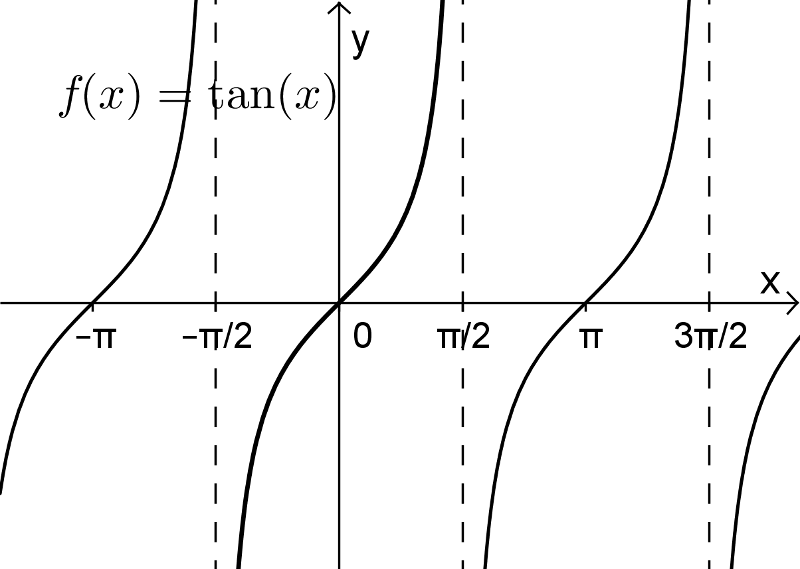

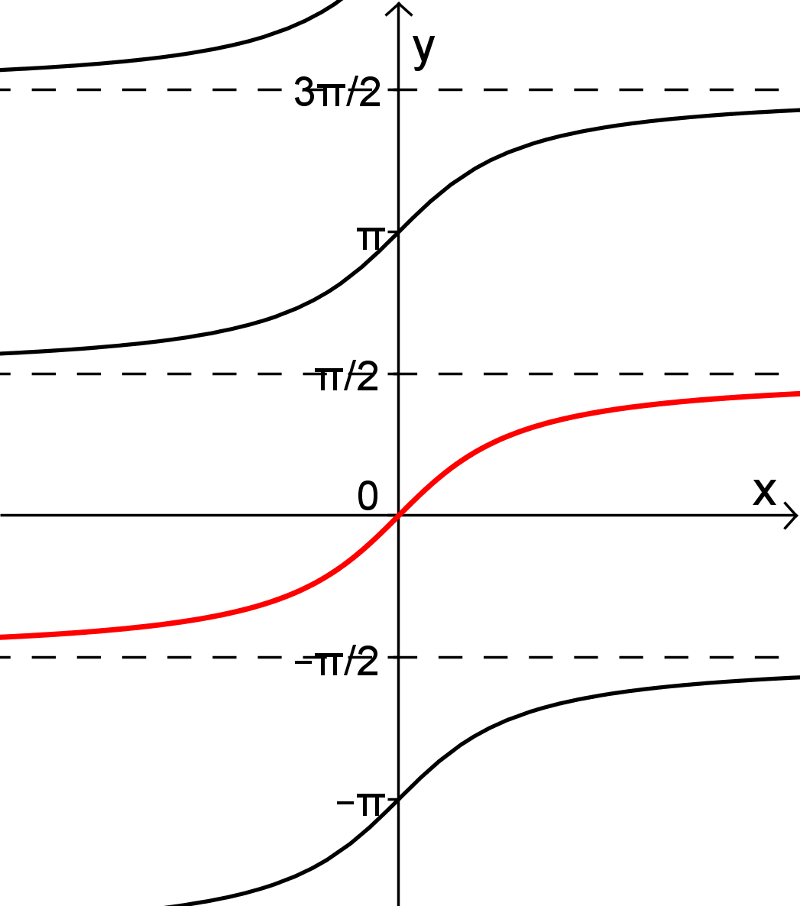
Nous pouvons alors définir la fonction arctangente de la façon suivante.
Exemple : Simplifiez l'expression 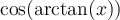 ,
,
En posant l'angle 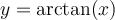 , on cherche donc à simplifier l'expression
, on cherche donc à simplifier l'expression 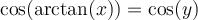 .
.
On a par définition que
Sachant que 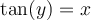 , on peut déterminer la valeur de
, on peut déterminer la valeur de 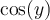 à l'aide de l'identité trigonométrique suivante :
à l'aide de l'identité trigonométrique suivante :
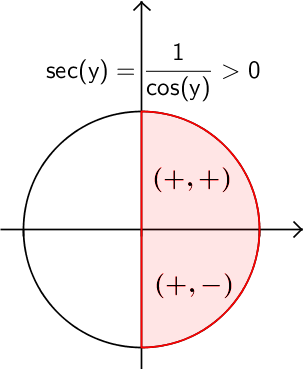
solution2 : À l'aide d'un schéma
Au lieu d'utiliser une identité trigonométrique, nous pourrions construire un triangle rectangle dont les côtés respectent la définition du rapport trigonométrique de tangente : 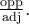
On sait que si 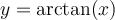 , alors
, alors 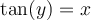 . On a donc
. On a donc
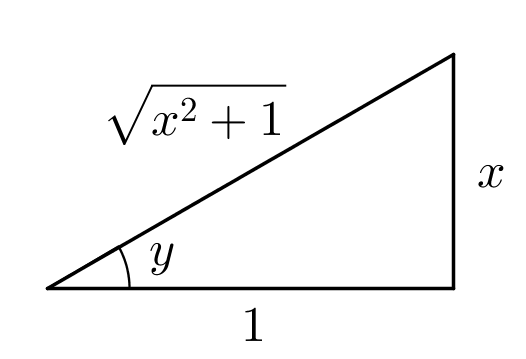
C'est-à-dire le côté opposé est égal à  et le côté adjacent est égal à
et le côté adjacent est égal à  . Par Pythagore, on a que l'hypoténuse doit être égale à
. Par Pythagore, on a que l'hypoténuse doit être égale à 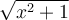 .
.
Ainsi,
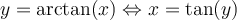
![y\in\left]-\frac{\pi}{2},\frac{\pi}{2}\right[ y\in\left]-\frac{\pi}{2},\frac{\pi}{2}\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/d3cb5a455333a1e5c4b61b0b6f16df51.png)
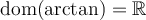
![\text{ima}(\arctan)=\left]-\frac{\pi}{2},\frac{\pi}{2}\right[ \text{ima}(\arctan)=\left]-\frac{\pi}{2},\frac{\pi}{2}\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/4a86e3c2bd8a8ef2553a806baf6c9379.png)
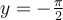
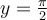
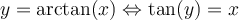
![y\in \left]-\frac{\pi}{2},\frac{\pi}{2}\right[ y\in \left]-\frac{\pi}{2},\frac{\pi}{2}\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/ddb9017d40ae21628b43743eca930757.png)
![\begin{array}{rll}\tan^2(y)+1&=\sec^2(y)&\\x^2+1&=\sec^2(y)&\small\text{; car }\tan(y)=x\\\sqrt{x^2+1}&=+\sec(y)&\small\text{ puisque }y\in\left]-\frac{\pi}{2},\frac{\pi}{2}\right[,\\[-0.5em]&&\small\text{ alors }\sec{y} > 0\\\sqrt{x^2+1}&=\dfrac{1}{\cos(y)}&\\\cos(y)&=\dfrac{1}{\sqrt{x^2+1}}&\end{array} \begin{array}{rll}\tan^2(y)+1&=\sec^2(y)&\\x^2+1&=\sec^2(y)&\small\text{; car }\tan(y)=x\\\sqrt{x^2+1}&=+\sec(y)&\small\text{ puisque }y\in\left]-\frac{\pi}{2},\frac{\pi}{2}\right[,\\[-0.5em]&&\small\text{ alors }\sec{y} > 0\\\sqrt{x^2+1}&=\dfrac{1}{\cos(y)}&\\\cos(y)&=\dfrac{1}{\sqrt{x^2+1}}&\end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/4eee0b9ee13ff14593f3a1442304fa17.png)