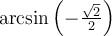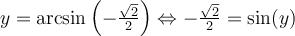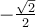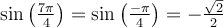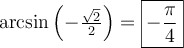3.3 Fonctions trigonométriques inverses
- Introduction
- Fonction arcsin
- Fonction arccos
- Fonction arctan
- Autres fonctions trigonométriques inverses
- Résoudre une équation trigonométrique
2. Fonction arcsin
Afin qu'une fonction  possède une fonction réciproque,
possède une fonction réciproque, 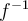 , il faut que
, il faut que  soit une fonction injective, c'est-à-dire qu´à toute valeur
soit une fonction injective, c'est-à-dire qu´à toute valeur 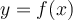 corresponde une seule valeur de
corresponde une seule valeur de  . Or, on constate que la fonction sinus n'est pas une fonction injective et donc ne possède pas de fonction réciproque.
. Or, on constate que la fonction sinus n'est pas une fonction injective et donc ne possède pas de fonction réciproque.
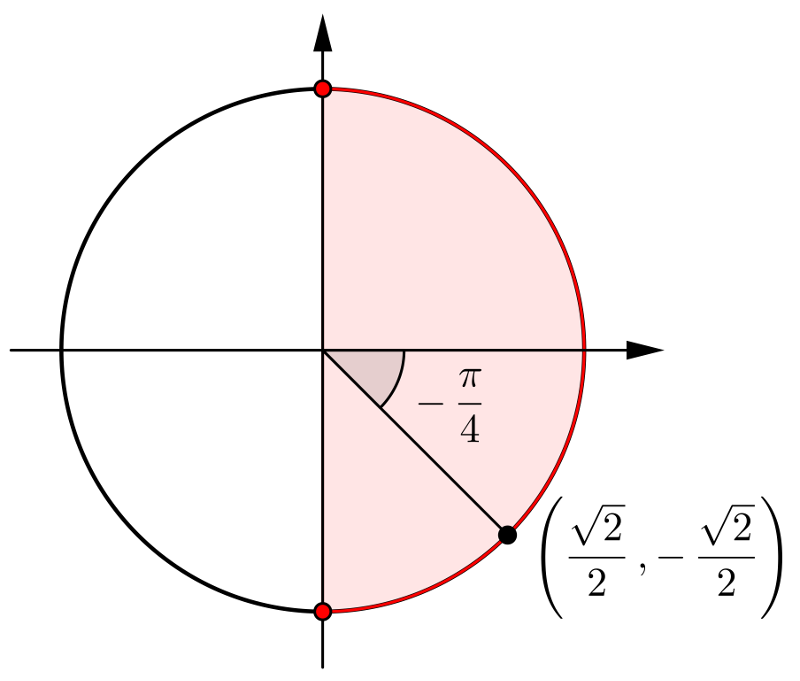
En effet, en observant le graphique de la fonction 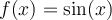 , il existe une droite horizontale qui coupe la courbe de sinus en plusieurs points d'intersection. Cela a comme conséquence que la courbe réciproque de sinus n'est pas une fonction par définition (voir le graphe de droite). Par exemple, il existe plus qu'une image
, il existe une droite horizontale qui coupe la courbe de sinus en plusieurs points d'intersection. Cela a comme conséquence que la courbe réciproque de sinus n'est pas une fonction par définition (voir le graphe de droite). Par exemple, il existe plus qu'une image  associée à la valeur
associée à la valeur 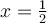 , soit entre autres,
, soit entre autres, 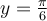 et
et 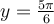 .
.
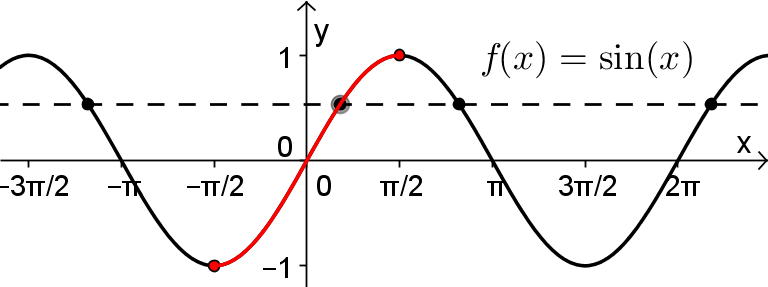

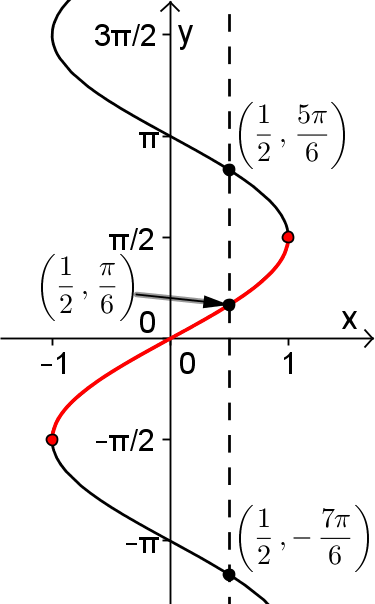
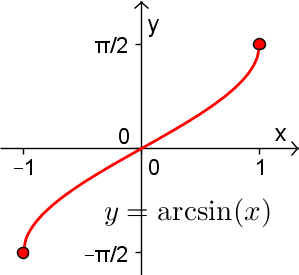
Par conséquent, pour créer la fonction réciproque arcsinus, il faut restreindre le domaine de sinus pour rendre cette fonction injective. Par convention, c'est sur l'intervalle des valeurs ![x\in\left[-\frac{\pi}{2},\frac{\pi}{2}\right] x\in\left[-\frac{\pi}{2},\frac{\pi}{2}\right]](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/0d192a1f8b4c6259ea6692cc0e8c2b65.png) qu'est définie notre fonction injective
qu'est définie notre fonction injective 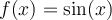 , représentée par la courbe rouge ci-dessus. Nous pouvons alors définir la fonction arcsinus de la façon suivante.
, représentée par la courbe rouge ci-dessus. Nous pouvons alors définir la fonction arcsinus de la façon suivante.
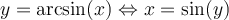
![y\in\left[-\frac{\pi}{2},\frac{\pi}{2}\right] y\in\left[-\frac{\pi}{2},\frac{\pi}{2}\right]](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/4a2da7ec8101d96f3f6dc9128b84a387.png)
![\text{dom}(\arcsin)=[-1,1] \text{dom}(\arcsin)=[-1,1]](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/7521eda7044f5661480e3f2eb1f81b53.png)
![\text{ima}(\arcsin)=\left[-\frac{\pi}{2},\frac{\pi}{2}\right] \text{ima}(\arcsin)=\left[-\frac{\pi}{2},\frac{\pi}{2}\right]](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/ffb3373e70ff9d2373fb614fdca9ac74.png)