3.2 Les identités trigonométriques
- Introduction
- Identités de base
- Formules trigonométriques utiles
- Formules d'addition d'angles
- Démonstration d'une identité
5. Démonstration d'une identité
On peut démontrer des identités plus complexes à l'aide des définitions des fonctions trigonométriques et des identités et formules démontrées précédemment. Il n'existe pas de démarche infaillible pour démontrer une identité, il faut souvent utiliser son intuition et son imagination, en se laissant guider par les opérations présentées et par les identités connues. En voici quelques exemples :
Exemples : Démontrons les identités suivantes.
Il faut tout d'abord exprimer tous les membres de cette équation en terme de sinus et cosinus. Nous allons développer le membre de droite de cette égalité, c'est-à-dire le transformer pour obtenir le membre de gauche.
L'identité est vérifiée.
Nous allons développer le membre de gauche de cette égalité pour obtenir celui de droite, car il est plus complexe, et par le fait même, peut se transformer plus facilement.
L'identité est vérifiée.
Nous allons développer le membre de gauche de cette égalité pour obtenir celui de droite, pour les mêmes raisons qu'à l'exemple précédent.
Tout d'abord, observons les identités connues qui pourraient nous être utiles, car elles contiennent des expressions qui se trouvent également dans l'identité à démontrer :
Nous allons utiliser les identités (1) et (3) pour développer notre membre de gauche.
L'identité est vérifiée.
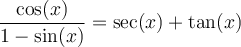
![\begin{array}{ll}\sec(x)+\tan(x)&\\[0.7em]=\dfrac{1}{\cos(x)}+\dfrac{\sin(x)}{\cos(x)}&\small{\text{; définition de }\tan(x)\text{ et }\sec(x)}\\[1em]=\dfrac{1+\sin(x)}{\cos(x)}&\\[1em]=\dfrac{(1+\sin(x))}{\cos(x)}\cdot\dfrac{(1-\sin(x))}{(1-\sin(x))}&\small\text{; multiplication par le conjugué du numérateur}\\[1em]=\dfrac{1-\sin^2(x)}{\cos(x)(1-\sin(x))}&\small ;\;(1+\sin(x))(1-\sin(x))=1-\sin^2(x)\\[1em]=\dfrac{\cos^2(x)}{\cos(x)(1-\sin(x))}&\small{\text{; identité }\cos^2(x)=1-\sin^2(x)}\\[1em]=\dfrac{\cos(x)}{1-\sin(x)}&\small{\text{; simplication par }\cos(x)}\\&\square\end{array} \begin{array}{ll}\sec(x)+\tan(x)&\\[0.7em]=\dfrac{1}{\cos(x)}+\dfrac{\sin(x)}{\cos(x)}&\small{\text{; définition de }\tan(x)\text{ et }\sec(x)}\\[1em]=\dfrac{1+\sin(x)}{\cos(x)}&\\[1em]=\dfrac{(1+\sin(x))}{\cos(x)}\cdot\dfrac{(1-\sin(x))}{(1-\sin(x))}&\small\text{; multiplication par le conjugué du numérateur}\\[1em]=\dfrac{1-\sin^2(x)}{\cos(x)(1-\sin(x))}&\small ;\;(1+\sin(x))(1-\sin(x))=1-\sin^2(x)\\[1em]=\dfrac{\cos^2(x)}{\cos(x)(1-\sin(x))}&\small{\text{; identité }\cos^2(x)=1-\sin^2(x)}\\[1em]=\dfrac{\cos(x)}{1-\sin(x)}&\small{\text{; simplication par }\cos(x)}\\&\square\end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/80d42dfbb4522a79b791708da3433a77.png)
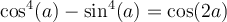
![\begin{array}{ll}\cos^4(a)-\sin^4(a)&\\[1em]=\left(\cos^2(a)+\sin^2(a)\right)\left(\cos^2(a)-\sin^2(a)\right)&\small\text{; il s'agit d'une différence de carrés}\\&\;\small u^2-v^2=(u+v)(u-v)\\&\small{\text{ où }u=\cos^2(a)\text{ et }v=\sin^2(a)}\\=(1)(\cos(2a))&\small{\text{; identités }\cos^2(a)+\sin^2(a)=1}\\&\;\small{\text{ et }\cos^2(a)-\sin^2(a)=\cos(2a)}\\=\cos(2a)&\\&\square\end{array} \begin{array}{ll}\cos^4(a)-\sin^4(a)&\\[1em]=\left(\cos^2(a)+\sin^2(a)\right)\left(\cos^2(a)-\sin^2(a)\right)&\small\text{; il s'agit d'une différence de carrés}\\&\;\small u^2-v^2=(u+v)(u-v)\\&\small{\text{ où }u=\cos^2(a)\text{ et }v=\sin^2(a)}\\=(1)(\cos(2a))&\small{\text{; identités }\cos^2(a)+\sin^2(a)=1}\\&\;\small{\text{ et }\cos^2(a)-\sin^2(a)=\cos(2a)}\\=\cos(2a)&\\&\square\end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/c24d120c915717a8fab24a1f48730d6f.png)
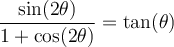
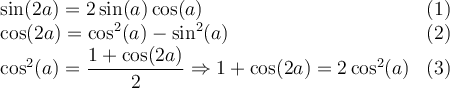
![\begin{array}{lll}\dfrac{\sin(2\theta)}{1+\cos(2\theta)}&=\dfrac{2\sin(\theta)\cos(\theta)}{2\cos^2(\theta)}&\small\text{; identités (1) et (3)}\\[1em]&=\dfrac{\sin(\theta)}{\cos(\theta)}&\small{\text{; simplification par }2\cos(\theta)}\\[1em]&=\tan(\theta)&\small\text{; définition de tangente}\\&&\square\end{array} \begin{array}{lll}\dfrac{\sin(2\theta)}{1+\cos(2\theta)}&=\dfrac{2\sin(\theta)\cos(\theta)}{2\cos^2(\theta)}&\small\text{; identités (1) et (3)}\\[1em]&=\dfrac{\sin(\theta)}{\cos(\theta)}&\small{\text{; simplification par }2\cos(\theta)}\\[1em]&=\tan(\theta)&\small\text{; définition de tangente}\\&&\square\end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/75a941aaa5e7415643a9239a7667264f.png)