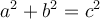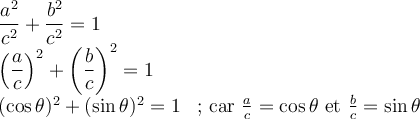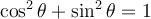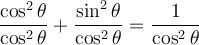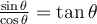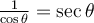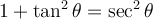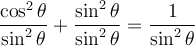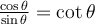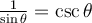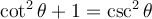3.2 Les identités trigonométriques: Identités de base | Mathéma-TIC

3.2 Les identités trigonométriques

Introduction
Identités de base
Formules trigonométriques utiles
Formules d'addition d'angles
Démonstration d'une identité

2. Identités de base

Soit le triangle

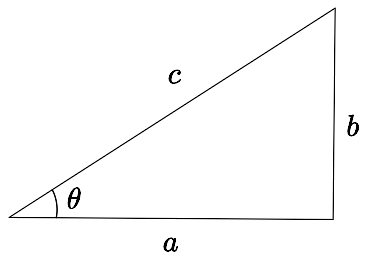
Triangle

L'identité à la base de toutes les autres s'appelle le théorème de Pythagore.

Théorème : Dans un triangle rectangle tel qu'illustré plus haut, on a toujours que

$a^2 + b^2 = c^2$

En divisant par 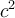$c^2$ de chaque côté, on obtient

$\begin{array}{ll}\dfrac{a^2}{c^2} + \dfrac{b^2}{c^2} = 1 &\\ \left(\dfrac{a}{c}\right)^2+\left(\dfrac{b}{c}\right)^2=1&\\(\cos\theta)^2+(\sin\theta)^2=1&\text{; car } \frac{a}{c}=\cos\theta\text{ et }\frac{b}{c}=\sin\theta\end{array}$

Par conséquent, en utilisant les définitions des fonctions trigonométriques, on obtient

$\cos^2\theta+\sin^2\theta =1$

Afin de trouver les deux autres identités de base, il suffit de diviser l'équation ci-dessus par 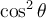$\cos^2\theta$ ou par $\sin^2\theta$ .

En effet,

$\dfrac{\cos^2\theta}{\cos^2\theta}+\dfrac{\sin^2\theta}{\cos^2\theta}=\dfrac{1}{\cos^2\theta}$

Comme $\frac{\sin\theta}{\cos\theta}=\tan\theta$ et $\frac{1}{\cos\theta}=\sec\theta$ , on peut déduire que

$1+\tan^2\theta=\sec^2\theta$

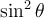$\dfrac{\cos^2\theta}{\sin^2\theta}+\dfrac{\sin^2\theta}{\sin^2\theta}=\dfrac{1}{\sin^2\theta}$

Comme $\frac{\cos\theta}{\sin\theta}=\cot\theta$ et $\frac{1}{\sin\theta}=\csc\theta$

$\cot^2\theta + 1=\csc^2\theta$