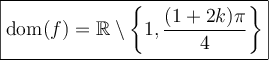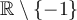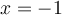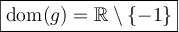3.1 La trigonométrie
- Définitions
- Angles remarquables
- Angles : degré et radian
- Cercle trigonométrique
- Fonctions trigonométriques et leur domaine
- Graphes des fonctions trigonométriques
5. Fonctions trigonométriques et leur domaine
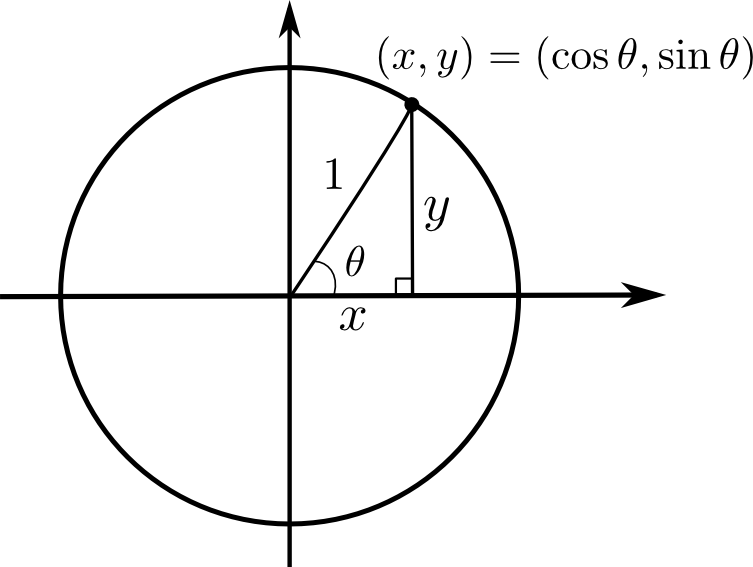
En utilisant ce que nous avons vu dans la section précédente, on définit les fonctions trigonométriques de la façon suivante.
Lorsque l'angle se situe entre  et
et 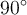 , le point est situé dans le premier quadrant et les définitions précédentes coïncident avec celles que nous avions données dans la section sur la trigonométrie du triangle.
, le point est situé dans le premier quadrant et les définitions précédentes coïncident avec celles que nous avions données dans la section sur la trigonométrie du triangle.
Recherche des domaines
Le domaine des fonctions sinus et cosinus est l'ensemble des 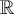 , car pour tout nombre réel
, car pour tout nombre réel  , les valeurs
, les valeurs 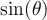 et
et 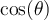 sont définies.
sont définies.
Par contre, il en est tout autre pour les valeurs de 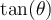 ,
, 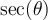 ,
, 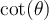 et
et 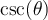 , car on peut voir dans le tableau ci-dessus que ces expressions sont définies uniquement si leur dénominateur n'est pas égal à 0. Il est donc très utile de connaître les angles
, car on peut voir dans le tableau ci-dessus que ces expressions sont définies uniquement si leur dénominateur n'est pas égal à 0. Il est donc très utile de connaître les angles  où les valeurs
où les valeurs 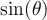 et
et 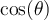 sont égales à 0. En fait, ces angles
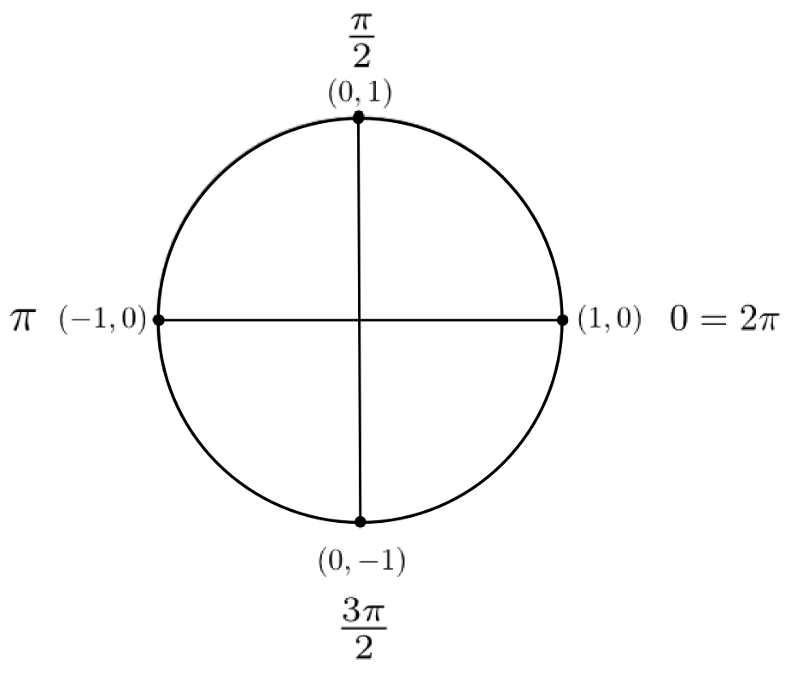
sont égales à 0. En fait, ces angles  sont ceux qui engendrent les points qui croisent les axes de coordonnées sur le cercle trigonométrique.
sont ceux qui engendrent les points qui croisent les axes de coordonnées sur le cercle trigonométrique.
La dernière ligne de chacun des tableaux indique que tous les angles qui annulent le cosinus ou le sinus sont nuls sont séparés par un angle de 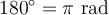 . On en déduit les domaines des autres fonctions trigonométriques.
. On en déduit les domaines des autres fonctions trigonométriques.
Exemples :
a) Trouver le domaine de la fonction 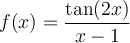 .
.
solution Réécrivons  en fonction de sinus et cosinus.
en fonction de sinus et cosinus.
Pour que  soit définie, il faut que le dénominateur soit
soit définie, il faut que le dénominateur soit 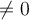 . On a que
. On a que
Par conséquent, le domaine de 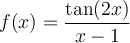 est :
est :
b) Trouver le domaine de la fonction 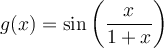
solution Il s'agit d'une fonction composée et son domaine dépend du domaine de 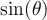 où
où 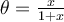 et du domaine de la fonction
et du domaine de la fonction 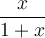 .
.
![\begin{array}{lrl}\bullet &\tan(\theta)&=\dfrac{\sin(\theta)}{\cos(\theta)}\\[2em]\bullet&\sec(\theta)&=\dfrac{1}{\cos(\theta)}\end{array} \begin{array}{lrl}\bullet &\tan(\theta)&=\dfrac{\sin(\theta)}{\cos(\theta)}\\[2em]\bullet&\sec(\theta)&=\dfrac{1}{\cos(\theta)}\end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/107791576d776fdaf8a17fa391aafd0d.png)
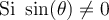
![\begin{array}{lrl}\bullet &\cot(\theta)&=\dfrac{\cos(\theta)}{\sin(\theta)}\\[2em]\bullet &\csc(\theta)&=\dfrac{1}{\sin(\theta)}\end{array} \begin{array}{lrl}\bullet &\cot(\theta)&=\dfrac{\cos(\theta)}{\sin(\theta)}\\[2em]\bullet &\csc(\theta)&=\dfrac{1}{\sin(\theta)}\end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/73096d79689f33ca6a5e9f9651511b46.png)
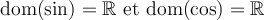
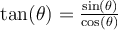
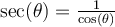
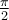
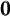
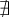
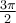
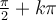
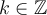
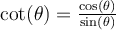
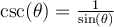
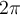
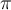
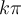
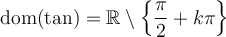
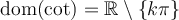
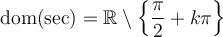
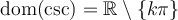
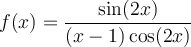
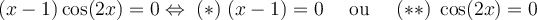
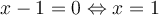
![\begin{array}{ll}\cos(2x)=0&\Leftrightarrow 2x=\dfrac{\pi}{2}+k\pi\text{ où }k\in\mathbb{Z},\\&\text{ car }\cos(\theta)=0\text{ si }\theta=\frac{-\pi}{2},\frac{\pi}{2},\frac{3\pi}{2},\dots\\[1em]&\Leftrightarrow x=\dfrac{\pi}{4}+\dfrac{k\pi}{2}=\dfrac{\pi+2k\pi}{4}=\dfrac{(1+2k)\pi}{4}\end{array} \begin{array}{ll}\cos(2x)=0&\Leftrightarrow 2x=\dfrac{\pi}{2}+k\pi\text{ où }k\in\mathbb{Z},\\&\text{ car }\cos(\theta)=0\text{ si }\theta=\frac{-\pi}{2},\frac{\pi}{2},\frac{3\pi}{2},\dots\\[1em]&\Leftrightarrow x=\dfrac{\pi}{4}+\dfrac{k\pi}{2}=\dfrac{\pi+2k\pi}{4}=\dfrac{(1+2k)\pi}{4}\end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/ac5c0808edae96763fc44d0f5967043d.png)