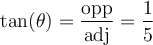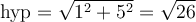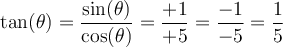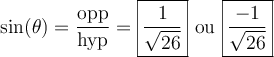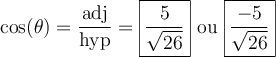3.1 La trigonométrie
- Définitions
- Angles remarquables
- Angles : degré et radian
- Cercle trigonométrique
- Fonctions trigonométriques et leur domaine
- Graphes des fonctions trigonométriques
4. Cercle trigonométrique
Considérons un cercle de rayon 1 et un point 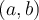 de ce cercle. Si le point est situé dans le premier quadrant, il détermine un triangle rectangle.
de ce cercle. Si le point est situé dans le premier quadrant, il détermine un triangle rectangle.
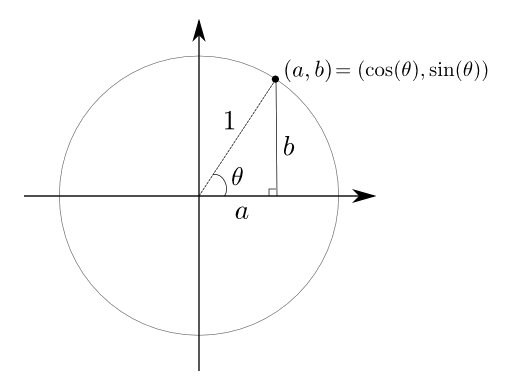
Étant donné ce que nous avons vu sur la trigonométrie dans le triangle, puisque l'hypoténuse mesure  unité, on déduit que
unité, on déduit que
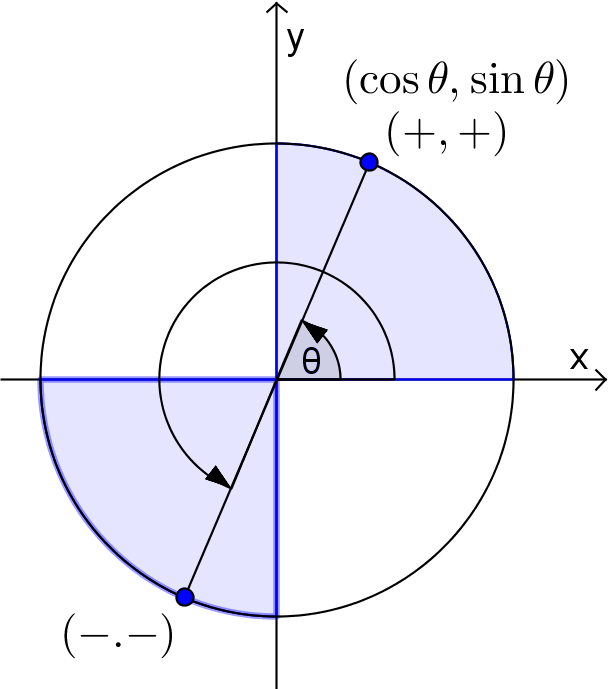
c'est-à-dire que la première coordonnée correspond au cosinus de l'angle et la deuxième, au sinus. On va étendre les définitions des fonctions trigonométriques en posant que 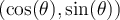 sont les coordonnées sur le cercle du point engendré par un angle de
sont les coordonnées sur le cercle du point engendré par un angle de  . De cette façon, on peut déduire les valeurs des angles remarquables en procédant par symétrie.
. De cette façon, on peut déduire les valeurs des angles remarquables en procédant par symétrie.
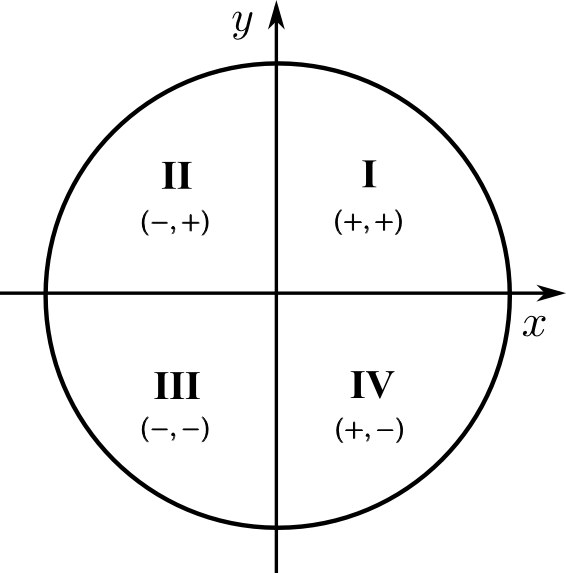
Les signes du sinus de  et du cosinus de
et du cosinus de  sont déterminés par la position du point sur le cercle, plus précisément par le quadrant dans lequel ce point est situé.
sont déterminés par la position du point sur le cercle, plus précisément par le quadrant dans lequel ce point est situé.
Tout d'abord, puisque le cercle est de rayon 1, il est facile de déduire qu'il coupe les axes aux coordonnées
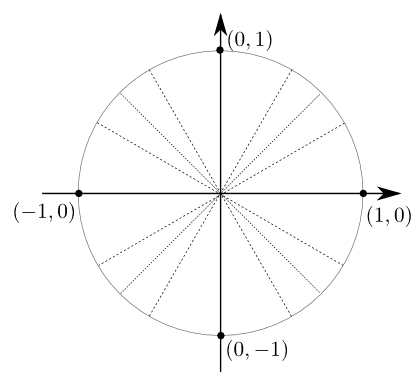
Ces points correspondent aux angles suivants en radians.
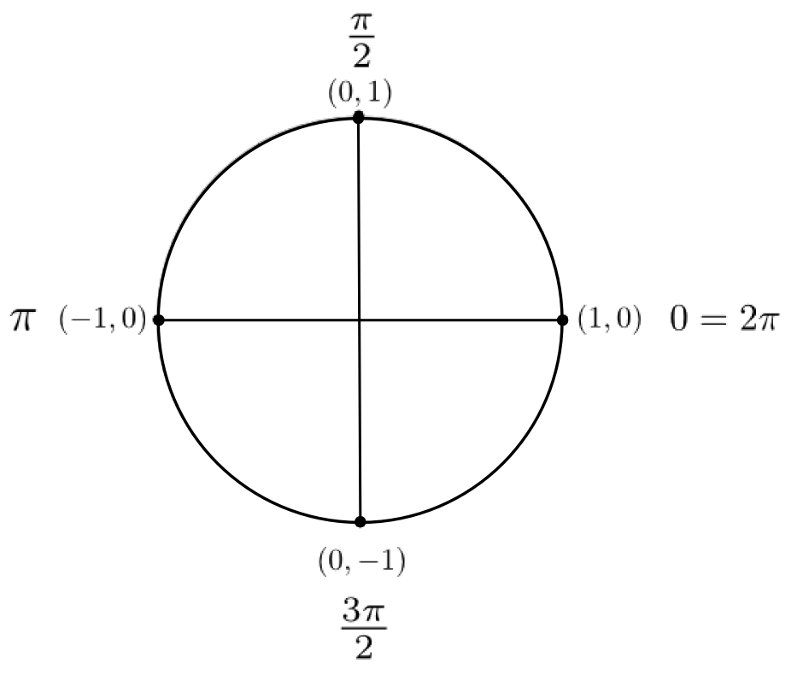
Étant donné ce que nous avons calculé précédemment dans la trigonométrie du triangle, on peut déduire les valeurs suivantes. En effet, la première coordonnée correspond au cosinus et la deuxième, au sinus de l'angle en question.
 |
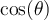 |
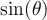 |
 ou ou 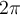 |
 |
 |
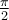 |
 |
 |
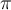 |
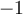 |
 |
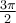 |
 |
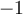 |
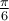 |
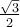 |
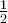 |
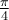 |
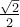 |
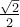 |
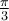 |
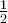 |
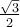 |
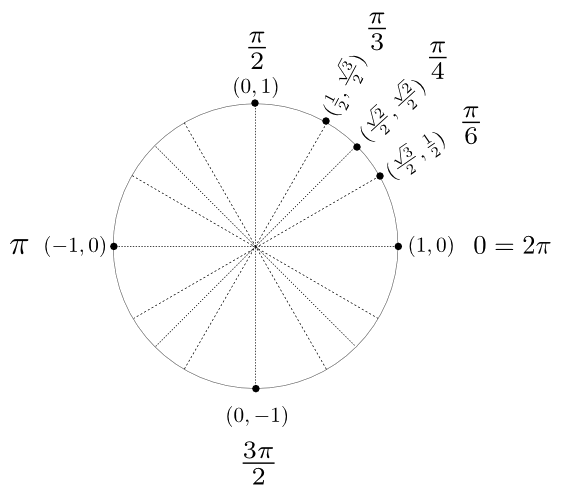
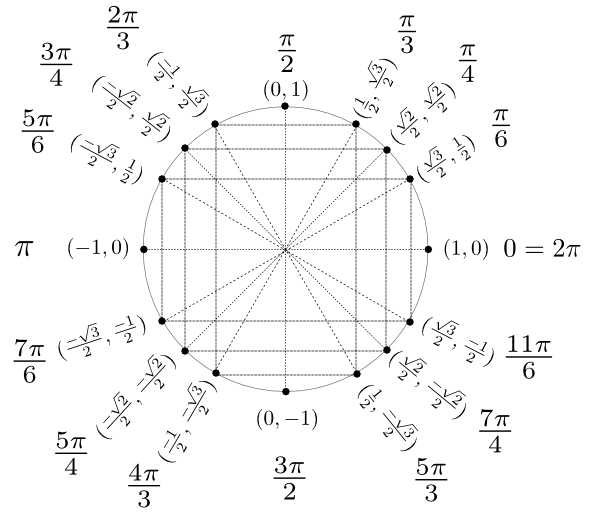
Par la suite, en procédant par symétrie, on peut déduire l'ensemble des valeurs particulières du cercle trigonométrique.
Exemple : Calculons les coordonnées du point P situé à un angle 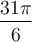 radians sur le cercle trigonométrique.
radians sur le cercle trigonométrique.
solution Chaque tour de cercle dans le sens antihoraire correspond à un angle de 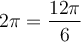 . Par conséquent,
. Par conséquent,
Les coordonnées du point 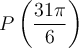 sont les mêmes que celles du point
sont les mêmes que celles du point 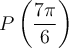 , soit
, soit 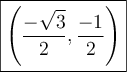 .
.
Exemple : Sachant que 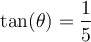 pour
pour ![\theta\in\left[0, 2\pi \right] \theta\in\left[0, 2\pi \right]](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/f8b5d3fbb3b4eb2a7ec3b6cd20f8108e.png) , déterminer les valeurs de
, déterminer les valeurs de 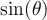 et
et 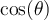 .
.
solution On sait que pour tout angle  , la fonction tangente est le rapport constant
, la fonction tangente est le rapport constant 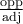 .
. Par conséquent, nous allons créer un triangle rectangle respectant ce rapport trigonométrique,
Par conséquent, nous allons créer un triangle rectangle respectant ce rapport trigonométrique,
Ainsi le côté opposé à l'angle est 1 et le côté adjacent est 5. Par le théorème de Pythagore, nous trouvons l'hypoténuse :
Étant donné que l'angle  prend des valeurs entre
prend des valeurs entre  et
et 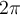 , les valeurs de
, les valeurs de 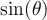 et
et 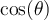 sont déterminées par les coordonnées des points sur le cercle situés dans le premier quadrant
sont déterminées par les coordonnées des points sur le cercle situés dans le premier quadrant 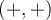 ou le troisième quadrant
ou le troisième quadrant 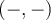 . En effet,
. En effet,
Ainsi, en lisant le triangle rectangle, on peut calculer les rapports demandés.
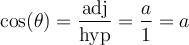
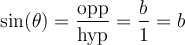
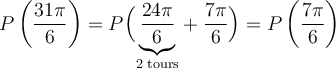

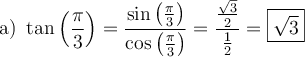
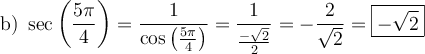

![\begin{array}{ll}\text{c) }\cot\left(\dfrac{-15\pi}{2}\right)&=\cot\Bigl(\underset{\text{3 tours}}{\underbrace{\dfrac{-12\pi}{2}}}+\dfrac{-3\pi}{2}\Bigr)\\[2em]&=\cot\left(\dfrac{-3\pi}{2}\right)=\cot\left(\dfrac{\pi}{2}\right)\\[1em]&=\dfrac{\cos\left(\frac{\pi}{2}\right)}{\sin\left(\frac{\pi}{2}\right)}\\[1em]&=\dfrac{0}{1}\\[1em]&=\boxed{0}\end{array} \begin{array}{ll}\text{c) }\cot\left(\dfrac{-15\pi}{2}\right)&=\cot\Bigl(\underset{\text{3 tours}}{\underbrace{\dfrac{-12\pi}{2}}}+\dfrac{-3\pi}{2}\Bigr)\\[2em]&=\cot\left(\dfrac{-3\pi}{2}\right)=\cot\left(\dfrac{\pi}{2}\right)\\[1em]&=\dfrac{\cos\left(\frac{\pi}{2}\right)}{\sin\left(\frac{\pi}{2}\right)}\\[1em]&=\dfrac{0}{1}\\[1em]&=\boxed{0}\end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/0137c006c88bf87ceeea4b8dc94e8410.png)