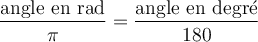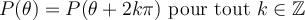3.1 La trigonométrie: Angles : degré et radian

3. Angles : degré et radian

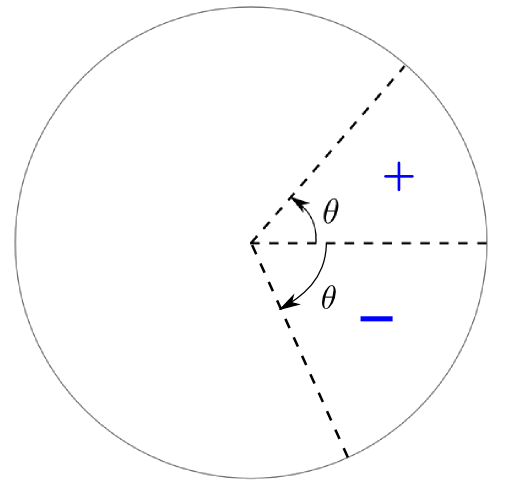
Lorsqu'on mesure les angles dans un cercle, par convention, le zéro est situé à droite à l'horizontale et on augmente dans le sens antihoraire tel qu'illustré dans la figure ci-dessous. Dans ce cas, la mesure de l'angle est positive, et elle est négative si la rotation se fait dans le sens horaire.

Deux façons de diviser le cercle sont largement répandues : les degrés et les radians.

Les degrés

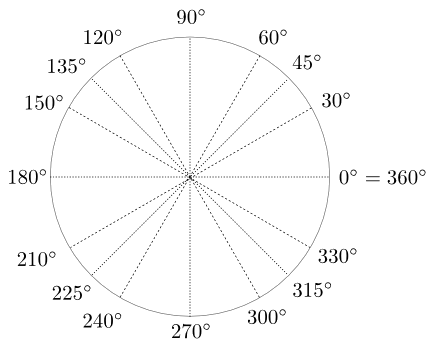
Dans le système de degré, on divise le cercle en 360 parties égales. Chacune de ces parties mesure 1 degré. Dans ce système, un angle droit mesure 90 degrés.

Les radians

Dans le système de radians, on mesure la longueur de la corde associée à l'angle en question dans un cercle de rayon 1. On a alors qu'un angle faisant un tour complet du cercle mesure 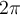$2\pi$ radians. L’intérêt majeur de ce système de mesure d'angle est de rattacher la mesure à un concept de longueur de la corde. Les principaux angles en radians sont

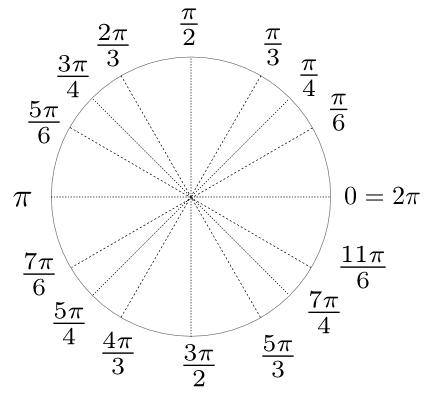
Le graphique Geogebra suivant explique de façon dynamique la notion d'angle en radian.

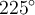Déplacez le point P sur le cercle de rayon 1. L'angle en radian correspond à la mesure de l'arc en bleu sur le cercle. Par exemple, si P fait un angle de $225^{\circ}$ , alors la longueur de l'arc en bleu est d'environ 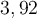$3,92$ radians, soit 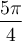$\dfrac{5\pi}{4}$ radians.

En continuant à déplacer le point P sur le cercle, vous passez sur les points correspondant aux différents angles remarquables et leurs équivalences en degrés et en radians.

Passer des radians aux degrés et vice versa

Pour passer d'un système de mesure à l'autre, il suffit d'effectuer une règle de 3. En effet, il y a un rapport de proportionnalité entre les radians et les degrés. Ainsi, puisque 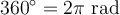$360^\circ = 2\pi\text{ rad}$

$\dfrac{\text{angle en rad}}{\pi}=\dfrac{\text{angle en degré}}{180}$

Par exemple, pour un angle 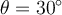$\theta=30^\circ$ , on a que 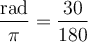$\dfrac{\text{rad}}{\pi}=\dfrac{30}{180}$ et donc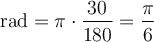 $\text{rad}= \pi\cdot\dfrac{30}{180} = \dfrac{\pi}{6}$

Les points trigonométriques égaux

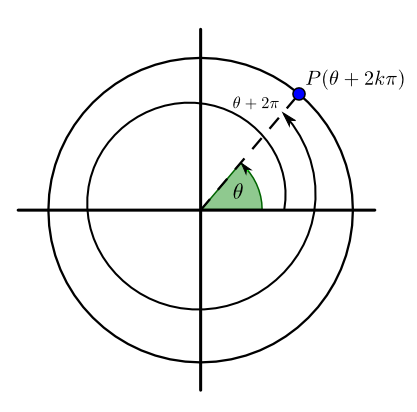
On constate qu'en partant d'un point sur le cercle et en effectuant des tours complets, on revient toujours au même point. Faire un tour complet signifie ajouter à un angle un multiple de 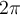$2\pi$ , ou $360^{\circ}$ .

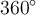On en déduit le résultat suivant :

$P(\theta)=P(\theta+2k\pi)\text{ pour tout }k\in\mathbb{Z}$

Centre d'Aide en Mathéma-TIC (CAM-TIC)