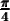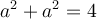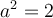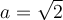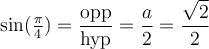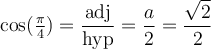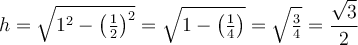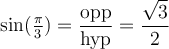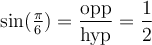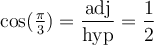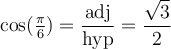3.1 La trigonométrie: Angles remarquables

3.1 La trigonométrie

Définitions
Angles remarquables
Angles : degré et radian
Cercle trigonométrique
Fonctions trigonométriques et leur domaine
Graphes des fonctions trigonométriques

2. Angles remarquables

Trois angles particuliers

Construisons un triangle rectangle isocèle, c'est-à-dire avec deux côtés égaux, et avec une hypoténuse de 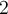$2$ . Les 2 angles autres que l'angle droit sont égaux et mesurent donc $45^{\circ}=\frac{\pi}{4}$ .

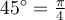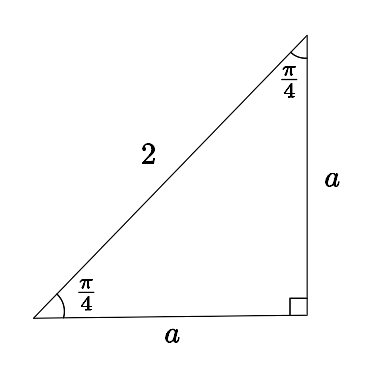
Dans ce cas, puisque les deux côtés sont égaux, on a, par Pythagore,

$a^2 + a^2 = 4$ et donc $a^2 = 2$ . On en déduit que $a=\sqrt{2}$ .

Comme le triangle est construit au complet, on peut déduire les valeurs des fonctions trigonométriques. Par exemple,

$\sin(\frac{\pi}{4})= \dfrac{\text{opp}}{\text{hyp}}=\dfrac{a}{2}=\dfrac{\sqrt{2}}{2}$

$\cos(\frac{\pi}{4})= \dfrac{\text{adj}}{\text{hyp}}=\dfrac{a}{2}=\dfrac{\sqrt{2}}{2}$ .

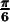Cas ( $\pmb{\frac{\pi}{6}}$ ou 30 degrés) et ( 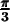$\pmb{\frac{\pi}{3}}$ ou 60 degrés)

Considérons maintenant un triangle équilatéral de côtés $1$ . Traçons la bissectrice à partir du sommet du haut. Nous obtenons le triangle

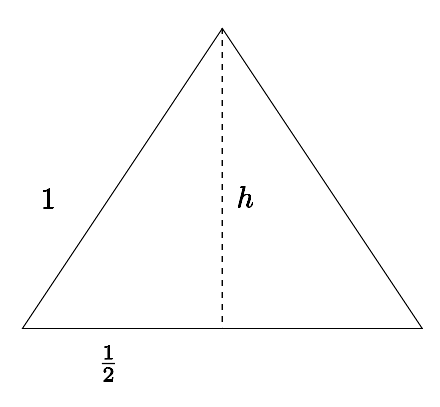
Cette bissectrice est aussi la médiatrice, car le triangle est équilatéral. Encore une fois, par Pythagore, on peut déduire que

$h=\sqrt{1^2-\left(\frac{1}{2}\right)^2} =\sqrt{1-\left(\frac{1}{4}\right)}=\sqrt{\frac{3}{4}}=\dfrac{\sqrt{3}}{2}$ .

Puisque le triangle équilatéral a 3 angles égaux (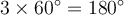 $3\times 60^{\circ}=180^{\circ}$ ) et que la bissectrice en coupe un en deux, on obtient le triangle

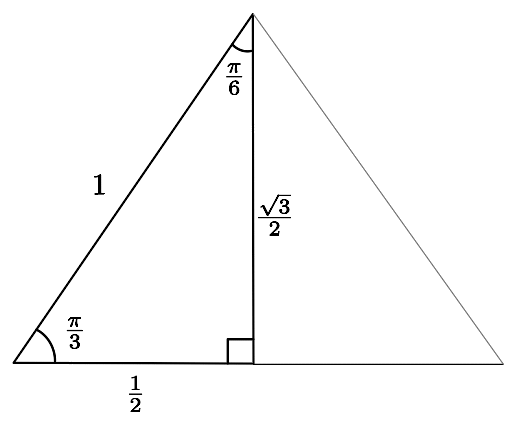
Il ne reste qu'à lire le triangle

$\sin(\frac{\pi}{3}) = \dfrac{\text{opp}}{\text{hyp}} = \dfrac{\sqrt{3}}{2}$

$\sin(\frac{\pi}{6}) = \dfrac{\text{opp}}{\text{hyp}} = \dfrac{1}{2}$

$\cos(\frac{\pi}{3}) = \dfrac{\text{adj}}{\text{hyp}} = \dfrac{1}{2}$

$\cos(\frac{\pi}{6}) = \dfrac{\text{adj}}{\text{hyp}} = \dfrac{\sqrt{3}}{2}$